Regressão Linear?

O termo “Regressão” surgiu em 1885 com o antropólogo, matemático e estatístico Francis Galton. As primeiras aplicações do método surgiram na Antropometria, ou seja, estudo das medidas e da matemática dos corpos humanos. Ao estudar as estaturas de pais e filhos, Galton observou que filhos de pais com altura baixa em relação à média tendem a ser mais altos que seus pais, e filhos de pais com estatura alta em relação à média tendem a ser mais baixos que seus pais, ou seja, as alturas dos seres humanos em geral tendem a regredir à média.

Regressão linear é um tipo de algoritmo supervisionado, portanto antes de entender como funciona o algoritmo é importante conhecer o que seria aprendizado supervisionado.

Conceitos importantes

Antes de prosseguir, há alguns conceitos importantes que precisam estar bem claros na sua mente.

• Variável independente ou preditora: é aquela que será passada para o modelo, tendo influência na variável que queremos encontrar. Por exemplo: Se queremos prever as vendas de sorvete, a estação do ano pode interferir nas vendas.
• Variável alvo ou dependente:é a variável que queremos prever. No exemplo acima seria as vendas de sorvete.

Aprendizado supervisionado?

O aprendizado supervisionado é aplicado quando tenta encontrar a relação entre a variável de alvo e as variáveis independentes. Uma das características mais importantes neste aprendizado é que os dados usados no treino do modelo devem ser “rotulados”, ou seja, nos dados de treino eu preciso ter os dados anotados com o valores corretos e nós sabemos do resultado de saída. Esse tipo de aprendizado é aplicado em 2 tipos de problemas: Classificação e Regressão. Um modelo de machine learning aprende os padrões dos dados e cria matematicamente uma função para gerar previsões, portanto pode-se afirmar que em algoritmos supervisionados a função para gerar os valores de resposta é:

Onde:

• f(x): é a função que o algoritmo irá criar.
• x: é a variável independente, ou seja, os atributos.
• yˆ: a saída estimada, com base na função.

---

Regressão Linear

Regressão linear é um algoritmo supervisionado de machine learning usado para estimar o valor de algo baseado em uma série de outros dados históricos, portanto olhando para o passado você pode “prever” o futuro.Existem 2 tipos de regressão linear: simples e a múltipla.

• Regressão linear simples: refere-se quando temos somente uma variável independente (X) para fazermos a predição.
• Regressão linear múltipla: refere-se a várias variáveis independentes (X)usadas para fazer a predição.

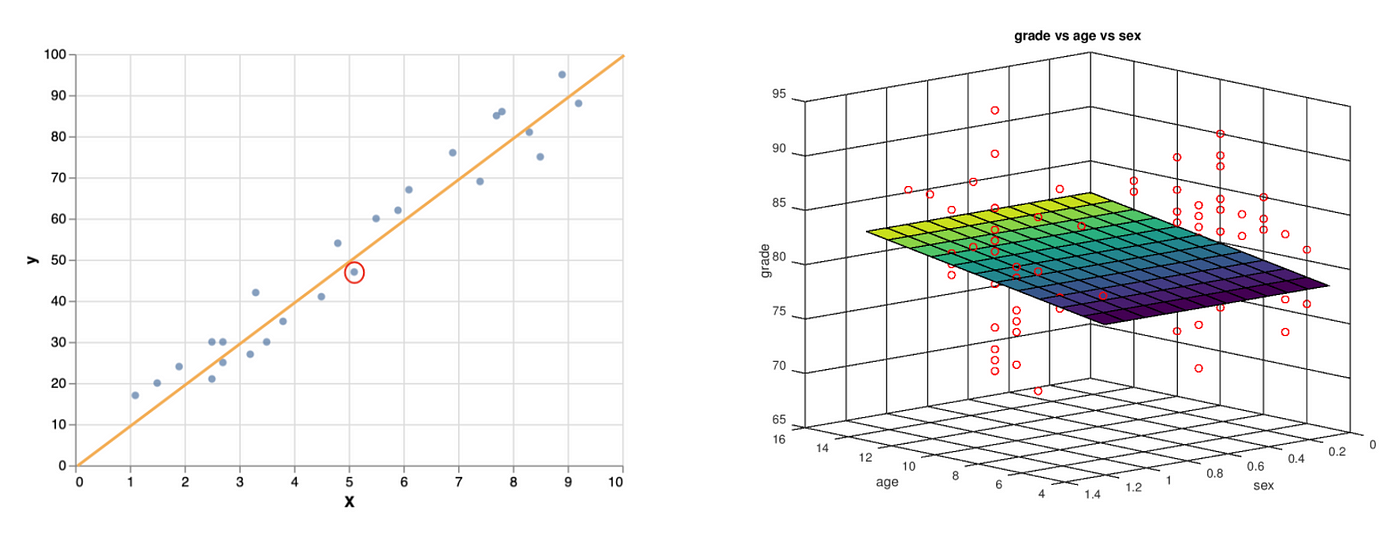
E com isso a forma de representação de cada regressão varia conforme o tipo, como por exemplo a representação gráfica em uma regressão linear simples é uma reta em um plano de 2 dimensões, já em uma regressão linear múltipla, sua representação é feita em um plano que pode ser nD.

---

Onde podemos usar regressão linear?

Esse algoritmo pode ser utilizado em qualquer problema, onde as variáveis de entrada e saída são valores contínuos. Por exemplo:

• Prever as vendas de um determinado produto
• Setor imobiliário (valor de um imóvel)
• Calcular a expectativa de vida de um país
• Calcular a pressão sanguínea de um paciente

---

Quando aplicar?

Esse tipo de algoritmo é aplicado quando há uma boa correlação linear (positiva ou negativa) entre os dados, ou seja, quando o relacionamento ou associação entre os dados pode ser definido com uma reta.

Mas o que é correlação?

É uma medida estatística utilizada para calcular a associação entre os pontos.

Correlação Linear de Pearson:mede a correlação linear entre a nuvem de pontos. O resultado varia entre -1 e 1:

• -1: Correlação linear perfeita negativa
• 1: Correlação linear perfeita positiva
• 0: Não tem correlação linear

---

O objetivo da regressão linear é encontrar uma reta que consiga definir bem os dados e minimizar a diferença entre o valor real e a saída calculada pelo modelo. A função que representa bem a regressão linear é dado a seguir:

Onde w0 (representa o ponto inicial da reta)e w1 (representa a inclinação da reta, ou seja, o quanto que essa variável cresce conforme o tempo passa) são variáveis que o algoritmo calcula para poder definir a reta, e x1 seria o atributo de entrada que foi dada ao modelo. E com esses valores ele consegue fazer as previsões.

Por exemplo, vamos supor que o algoritmo calculou o valor de w0 e w1 e definiu que seria respectivamente 0 e 10. O valor de x1 será 5.1, portanto o cálculo realizado será:

Yˆ= f(x) =0 + 10 * 5.1

Yˆ= 51

Esse cálculo será realizado para todas as previsões que serão realizadas, portanto se plotar essas previsões, chegará no seguinte gráfico:

Os pontos azuis representam os valores reais, já a reta representa a reta estimada pelo modelo. Note que no ponto circulado em vermelho é o valor real, da variável que calculamos anteriormente, e chegamos a um valor de 51, já o valor real é de mais ou menos 49, portanto há um erro no valor estimado do modelo.

Se você fizer o valor real menos o valor previsto, poderá obter o erro/ resíduo. Portanto a equação ficaria:

residuo = Y - Yˆ

No nosso caso o resíduo é -2 para esse ponto em específico.O resíduo representa a quantidade da variabilidade que Y que o modelo ajustado não consegue explicar. Os resíduos contém informação sobre o motivo do modelo não ter se ajustado bem aos dados.

---

Métricas de validação

SQR (Soma dos Quadrados dos Resíduos)

Soma dos quadrados dos resíduos, mostra a variação de Y que não é explicada pelo modelo elaborado. É a medida da variação que não pode ser explicada.

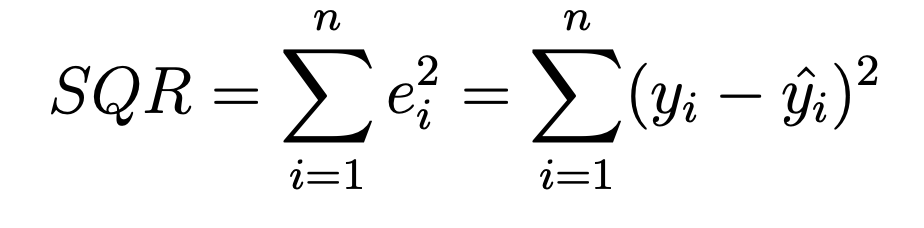
R²

O R² é uma medida estatística de quão próximos os dados estão da linha de regressão ajustada. Ele também é conhecido como o coeficiente de determinação ou o coeficiente de determinação múltipla para a regressão múltipla.

O R² está sempre entre 0 e 1:

• 0: indica que o modelo não explica nada da variabilidade dos dados de resposta ao redor de sua média.
• 1: indica que o modelo explica toda a variabilidade dos dados de resposta ao redor de sua média.

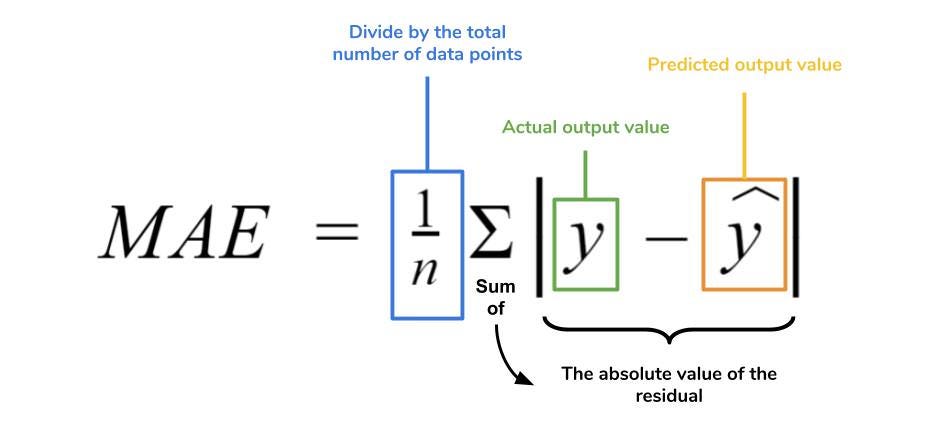
MAE (Erro Médio absoluto)

O erro médio absoluto (MAE) é a métrica de erro de regressão mais simples de entender. Ele calcula o valor dos resíduos para cada um dos pontos e depois é tirado a média de todos esses resíduos.

MSE (Média dos erros ao quadrado)

O MSE é apenas o cálculo do erro mas elevamos ao quadrado.

Por estarmos elevando o resíduo ao quadrado, não podemos comparar ele com o valor de MAE, pois ele sempre será maior portanto faz mais sentido comparar o MSE com o valor do MSE de outro modelo.

---

Exemplo com python

Neste exemplo tentaremos prever a nota de matemática das pessoas que fizeram o Enem em 2016.

Essa é a carinha do dataframe:

No dataframe há 167 colunas e 13730 linhas, mas será que vamos usar todas essas colunas para prever a nota de matemática?

Após uma série de análises (que você poderá visualizar no repositório do Github), eu fui descartando algumas colunas como por exemplo: Número da inscrição, ano da prova, município de residência, Estado, etc.

Mas uma forma mais fácil de selecionar as variáveis independentes para o modelo de regressão, é calcular a correlação entre elas e a variável alvo.

E com isso podemos selecionar as seguintes variáveis: ‘NU_NOTA_CN’,’ NU_NOTA_CH’, ’NU_NOTA_LC’, ’NU_NOTA_REDACAO’.

Para criar o algoritmo de regressão linear, irei utilizar a biblioteca scikit-learn.

Neste trecho, eu instanciei o modelo de regressão linear, e declarei as variáveis que serão utilizadas. Após isso eu quebrei ambas variáveis em treino e teste, onde 30% dos dados ficou para teste e 70% ficou para treino

E para gerar o treinamento do modelo é só utilizar a função .fit( ), passando por parâmetro os dados X e Y de treino.A função .score( ) retorna o valor de R²:

Para testar o modelo é utilizado a função .predict( ), passando por parâmetro os dados X de teste.

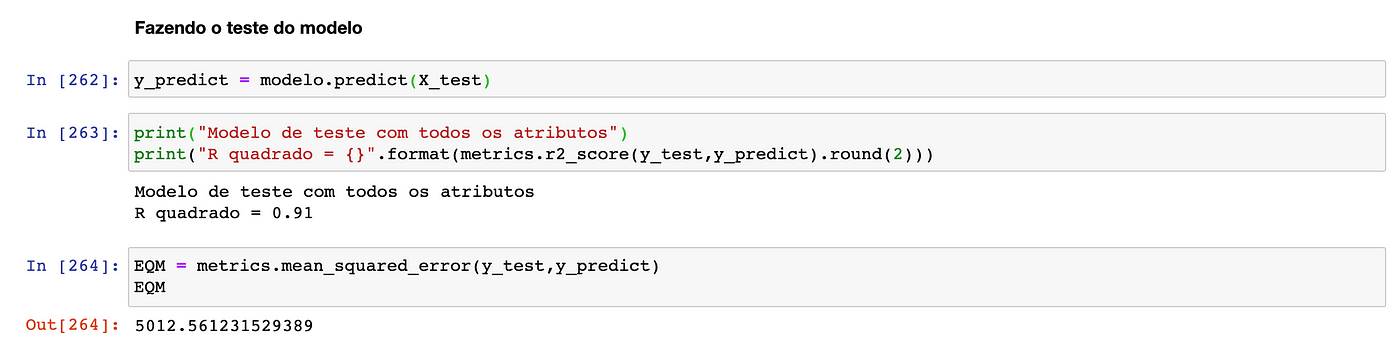
Se lembram da equação da regressão linear?

Para pegar os valores de w0, é utilizado a função .intercept_, já os valores de w1 pode ser adquirido com a função .coef_.

Como ficaria a equação no nosso modelo?

    
        f(NU_NOTA_CN, NU_NOTA_CH, NU_NOTA_LC, NU_NOTA_REDACAO) = -5.255134 + 0.335875 * Nota de ciências naturais -0.135485 * Nota de ciências humanas + 0.560740 * Nota de LC + 0.083826 * Nota da redação
    

Mas Laura porquê você selecionou as variáveis pro modelo?

Quando fazemos a seleção de features evitamos que atributos irrelevantes podem causar um efeito negativos no modelo, e além disso evitar a maldição da dimensionalidade, portanto à medida que aumenta o número de dimensões de seus dados, eles se tornam mais esparsos, o que pode dificultar a obtenção de um padrão.

Pois bem, mas vamos testar com as 15 features que a gente plotou na matriz de confusão: ‘TP_ESCOLA’,’TP_PRESENCA_CH’,’TP_PRESENCA_CN’,’TP_PRESENCA_LC’,’NU_IDADE’,’TP_ST_CONCLUSAO’, ’TP_ANO_CONCLUIU’, ‘TP_ENSINO’,’IN_TREINEIRO’,’NU_NOTA_CN’,’NU_NOTA_CH’,’NU_NOTA_LC’,’TP_STATUS_REDACAO’,’NU_NOTA_REDACAO’

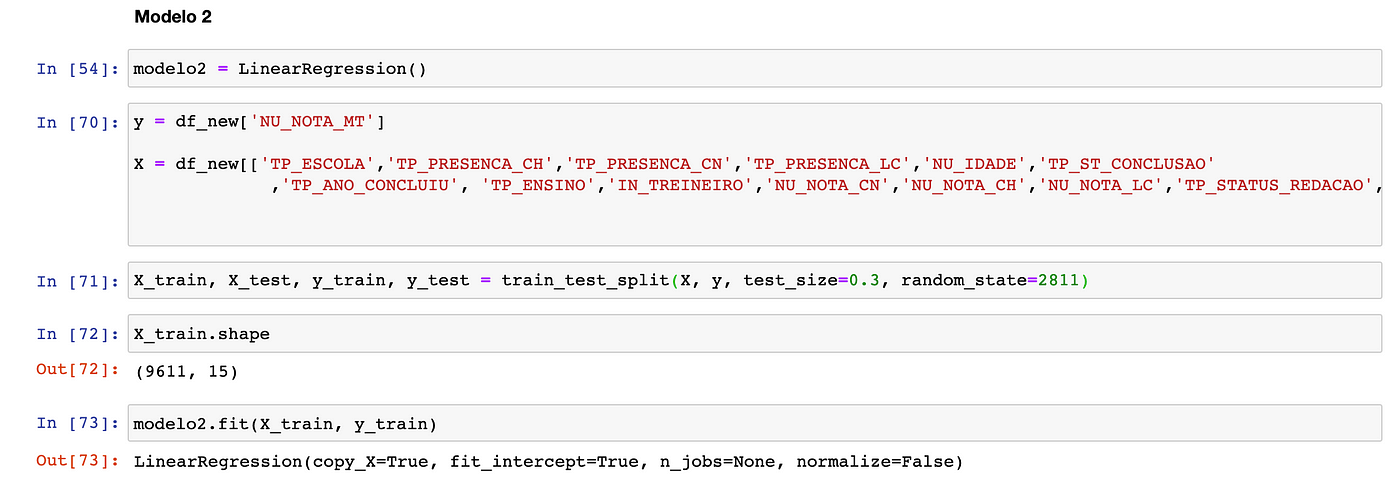
Vocês perceberam que o resultado de R² é o mesmo que com a seleção de atributos que fizemos anteriormente? Olha só, com 5 features conseguimos ter o mesmo resultado ao utilizar 15 features, perceberam a diferença?

---

Então foi isso galera, para acessar o código utilizado neste artigo basta clicar aqui! Qualquer dúvida ou feedback podem me chamar!